Table of contents
I'm developing a game that has a map design involving hex tiles connected in a graph along the edges. In my case, the hex tiles represent a sort of "watch tower", and the edges connecting them represent walls that are impassable without first addressing the towers. You can see the general idea in the prototype image above.
I found the solution to be challenging and algorithm-heavy, and I didn't find much help online for this particular problem. If you are wanting to accomplish something similar, I hope this short write-up can help you out.
Preamble
While I am working in Unity with C#, this barely touches any Unity specifics and should apply to any game engine, programming language, or library.
I did not implement the basic, "solved" parts of the hex math, and neither should you. I found this excellent MIT-licensed library for hex math, which takes many of its ideas from what is essentially the canonical source on hex algebra here. If you're reading this and haven't yet learned your hex basics, read that first.
I'm using point-topped hexes, but this applies just as well to flat-topped hexes. However, be aware that Unity's flat-top hex grid uses X as the vertical axis, which no other library (or sane person) would do, so it may cause you extra headache.
This very well may not be the best way of approaching the problem -- feel free to let me know what I may have missed.
Defining The Edges
Overview
The basic strategy of our algorithm is this:
Given two different hex cells A and B on a hex grid,
Find a shortest valid line of hex cells between A and B (there are very often multiple valid shortest lines, just pick one).
For each cell in that line (excluding A and B themselves), observe its six direct neighbors. Find the "short side" of neighbors, defined as the smallest group of neighbors on either side of the line.
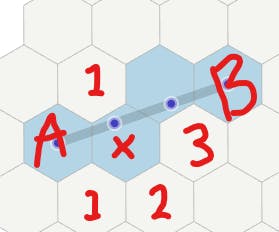
- Take for example the image above. We are drawing an edge from cells A to B, and start by observing X. Of its neighbors, there is a single one on the top side of the line, and 3 on the bottom. So, we choose the top.
For each selected neighbor add an edge in our result set of edges, where an edge is defined as two adjacent hex cells.
Repeat this process for each cell in the line. You should end up with this:
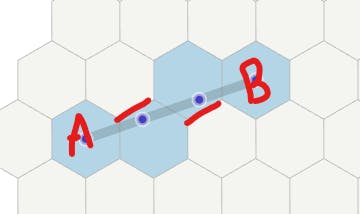
There's one glaring issue here: Where the two center cells connect, an edge is missing from the line. This happens when we "switch sides", so to speak. The first link in the line had its edge defined on top, while the second had its edge defined on the bottom. In those cases we need a cross-over edge. To accomplish this we add another small bit of logic:
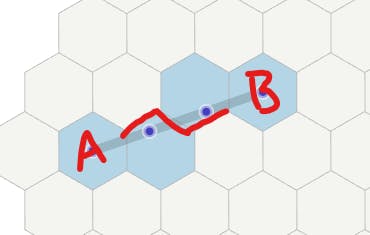
When defining the edges created by a cell in our line, first find the short-side edges as usual. Now, look back at our existing edges. We should have at least one new edge that shares a cell with the already-defined edges (remember, an edge is defined simply as two adjacent cells). If that isn't the case, add an edge between the current cell and the previous one. And we have our result!
Code
The strategy is a little heady. Here's some concrete code to help clarify. First, some simple data classes to hold our results:
// A container class for our result
public class HexPath {
public HexOffsetCoordinates endpointOne;
public HexOffsetCoordinates endpointTwo;
public List<HexEdge> edges;
}
// A simple definition of an edge as two adjacent cells.
// Note, this could be erroneous and hold two non-adjacent cells. If you like
// feel free to add validation logic, or define an edge as, for example, a
// single cell and a direction.
public struct HexEdge {
public HexOffsetCoordinates borderCellOne;
public HexOffsetCoordinates borderCellTwo;
}
Now, we get into the real meat
public class HexPathGenerator {
// It's convenient to have a list of directions to work with later
private static readonly List<Direction> Directions = new() {
Direction.NorthWest,
Direction.NorthEast,
Direction.East,
Direction.SouthEast,
Direction.SouthWest,
Direction.West,
};
// Our main method.
public HexPath GeneratePath(HexOffsetCoordinates fromCell, HexOffsetCoordinates toCell) {
var result = new List<HexEdge>();
var path = HexLibrary.GetLine(fromCell, toCell);
// Ignore first and last, iterate through the cells between.
for (var i = 1; i < path.Length - 1; i++) {
foreach (var neighbor in GetShortSideNeighbors(result, path[i], path[i - 1], path[i + 1], i != 1)) {
result.Add(new HexEdge(neighbor, path[i]));
}
}
return new HexPath {
endpointOne = fromCell,
endpointTwo = toCell,
edges = result,
};
}
private List<HexOffsetCoordinates> GetShortSideNeighbors(
List<HexEdge> currentEdges,
HexOffsetCoordinates cell,
HexOffsetCoordinates previousNeighbor,
HexOffsetCoordinates nextNeighbor,
bool handleContinuity) {
var neighborOneDirection = GetDirectionIndex(cell, previousNeighbor);
var neighborTwoDirection = GetDirectionIndex(cell, nextNeighbor);
if (neighborOneDirection == -1 || neighborTwoDirection == -1) {
// A hopefully-impossible error case
return new List<HexOffsetCoordinates>();
}
var setOne = GetNeighborDirectionsBetween(neighborOneDirection, neighborTwoDirection);
var setTwo = GetNeighborDirectionsBetween(neighborTwoDirection, neighborOneDirection);
var workingSet = setOne.Count switch {
// When both sides are of equal length, pick whichever one has a higher-indexed direction in it.
// This should mean there's a tendency for all paths to err in the same direction, and therefore
// overlap more, instead of creating weird 1-hex pockets.
var count when count == setTwo.Count => setOne.Max() > setTwo.Max() ? setOne : setTwo,
var count when count > setTwo.Count => setTwo,
_ => setOne,
};
var result = workingSet
.Select(directionIndex => HexLibrary.GetNeighbor(cell, Directions[directionIndex]))
.ToList();
// Handle weirdness where we may be switching "sides" and need a crossover edge.
// This is all wrapped in the handleContinuity boolean as a messy way to avoid performing this logic on the first cell in the line, for which it will be excessive.
if (handleContinuity) {
var isContinuousPath = false;
foreach (var edge in currentEdges) {
if (result.Contains(edge.borderCellOne) || result.Contains(edge.borderCellTwo)) {
isContinuousPath = true;
}
}
if (!isContinuousPath) {
result.Add(previousNeighbor);
}
}
return result;
}
private int GetDirectionIndex(HexOffsetCoordinates reference, HexOffsetCoordinates adjacentCell) {
for (int i = 0; i < Directions.Count; i++) {
if (HexGridUtils.HexLibrary.GetNeighbor(reference, Directions[i]) == adjacentCell) {
return i;
}
}
Debug.LogError($"Unable to find direction, cell ({reference}) must not be adjacent to {adjacentCell}");
return -1;
}
private List<int> GetNeighborDirectionsBetween(int indexOne, int indexTwo) {
var result = new List<int>();
var currentIndex = indexOne + 1;
while (currentIndex % Directions.Count != indexTwo) {
result.Add(currentIndex % Directions.Count);
currentIndex++;
}
return result;
}
}
The code is far from cleanly handling every edge case, but it gets the job done and should be a great jumping-off point for anyone that wants to accomplish something similar.
Drawing the Lines
Now the only part of the process left is to draw the lines to the screen. As of yet, we have defined everything in terms of hex grid coordinates, so this will rely on ways to convert to "world" or screen coordinates. This will vary somewhat depending on your environment.
First, we add a simple helper to HexEdge to get its vertices
public struct HexEdge {
// This is whatever your hex is defined as in-world. This, for example, is the Unity default
private static readonly Vector3 HexCellSize = new(0.8659766f, 1, 1);
public HexOffsetCoordinates borderCellOne;
public HexOffsetCoordinates borderCellTwo;
// The parameter is a function which converts hex coords to world coords.
// In Unity, this should be Grid.CellCenterWorld().
public List<Vector3> WorldVertices(Func<Vector3Int, Vector3> cellCenterWorld) {
var verticesOne = HexGridUtils.HexTileVertices(cellCenterWorld(borderCellOne.AsVector3Int()));
var verticesTwo = HexGridUtils.HexTileVertices(cellCenterWorld(borderCellTwo.AsVector3Int()));
var commonVertices = new List<Vector3>();
foreach (var vertex in verticesOne) {
foreach (var vertex2 in verticesTwo) {
// Here I'm using an extension for floats to prevent floating point precision errors.
if (vertex.AboutEquals(vertex2)) {
commonVertices.Add(vertex);
break;
}
}
}
if (commonVertices.Count != 2) {
Debug.LogWarning($"Expecting two common vertices for any adjacent tiles. {borderCellOne}, {borderCellTwo}");
}
return commonVertices;
}
private static List<Vector3> HexTileVertices(Vector3 worldCenter) {
var halfWidth = HexCellSize.x / 2;
var quarterHeight= HexCellSize.y / 4;
// Starting NW corner, moving clockwise.
return new List<Vector3> {
worldCenter + new Vector3(-halfWidth, quarterHeight, 0),
worldCenter + new Vector3(0, quarterHeight * 2, 0),
worldCenter + new Vector3(halfWidth, quarterHeight, 0),
worldCenter + new Vector3(halfWidth, -quarterHeight, 0),
worldCenter + new Vector3(0, -quarterHeight * 2, 0),
worldCenter + new Vector3(-halfWidth, -quarterHeight, 0),
};
}
From there, it's a simple matter of drawing all the vertices in whatever your preferred manner may be. For my rudimentary prototype, I just use a simple Unity LineRenderer.
That's all! Feel free to get in contact for any comments, questions, or concerns.

